矩阵乘法与线形变换的复合变换
了解了线形变换后~ 那么这一次我们加一些更为复合的变换! 也就是多次变换!
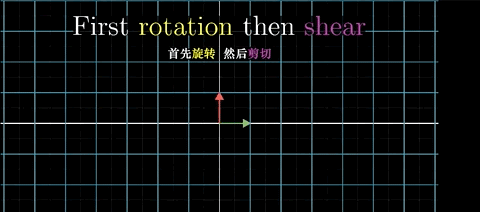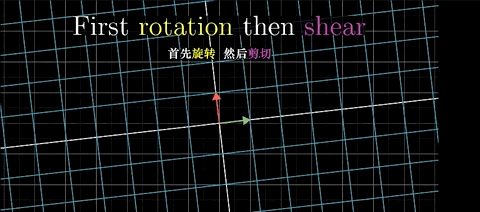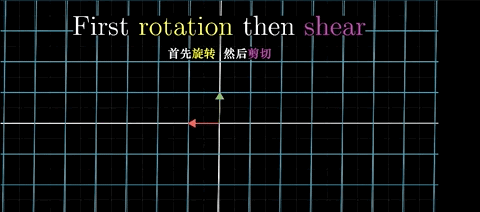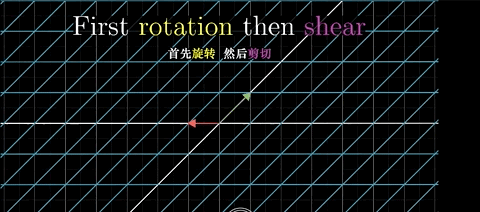
这里我们先从函数的角度去考虑!
比如定义对应的两个函数分别为旋转函数 fR 和剪切函数fS,需要算得的变换后的任意向量当做一个参数定义为a
因为上面变换过程是先旋转然后再剪切,那么使用函数表达就应该是下面的样子
fS(fR(a))
首先进行旋转矩阵的计算,然后将计算后的结果再进行剪切矩阵的计算!
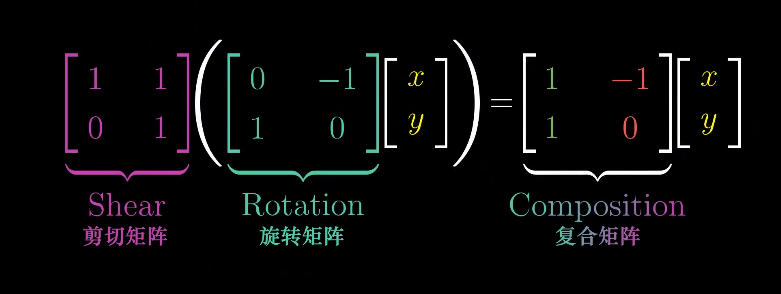
这就是复合矩阵的计算公式!是如何推算出来的呢?我们先去除任意向量的参数,只去考虑基向量的运算!把基向量的变换算出来,那么其张成空间中的任意向量就理所当然的可以算出!
看看复合矩阵的结果是如何计算出来的!
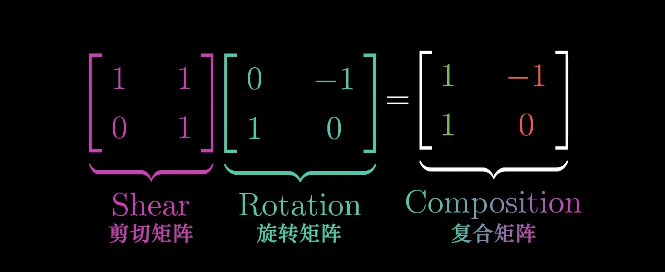
时刻记得两个矩阵相乘有着几何意义!也就是两个线形变换作用的过程!
首先我们把旋转后的矩阵当做最初始的矩阵! i (0,1), j (-1,0)
我们先去算出 i 帽 (0,1)基向量经过剪切变换后的矩阵坐标!!
根据之前学习的知识他的计算过程是这样的!
[01][1011]=0[10]+1[11]=[0+10+1]=[11]
这样就算出旋转矩阵的 i 帽向量,经过剪切矩阵变换后的向量坐标了!同样的我们给出 j帽的计算过程!
[−10][1011]=−1[10]+0[11]=[−1+00+0]=[−10]
将i帽和j帽组合就是我们的复合矩阵的结果了! 也就是经过旋转矩阵和剪切矩阵后的复合矩阵!代表了经过复合变换后,i帽向量和 j 帽向量的位置!
[11−10]
将上面的计算过程总结为公式:
[acbd][egfh]=>[ae+bgce+dgaf+bhcf+dh]
看到这里是不是能理解这个公式是如何来的了!而不是死记硬背他!
要理解背后复合变换的几何意义,每次计算前就算记不住公式,也可以大致的回顾一下这个复合变换的集合过程!理解其背后的实际意义!

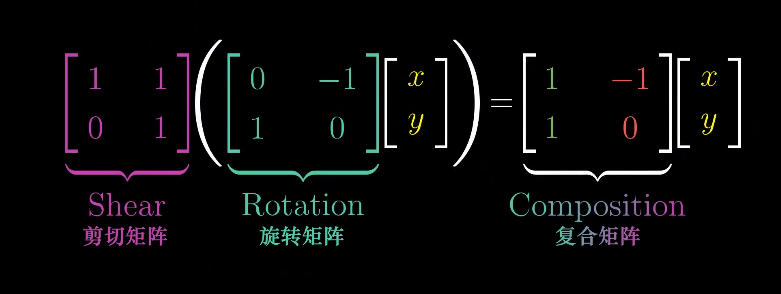




评论区