矩阵与线性变化

目标：理解而不是死记硬背矩阵向量相乘的原理！

线性变换

变换本质是函数的另一种说法，接受一个处理并输出结果

变换这个词，让你以可视化的思维去理解这个输入输出的过程！

如果一个变换，输入一个向量，然后输出一个向量，我们就去想象一个向量，从输入向量位置移动到输出向量位置的过程！

任意的变换可能非常复杂！所以线性代数中的变换限制在一种特殊的变换机制中！这也是他为什么叫线性代数的原因！

如果变化具有一下两种特质，我们就称这个变换为线性的！

• 直线在变换后仍然是直线，不能有所弯曲！
• 原点必须保持固定！

如何用数值描述线性变换？

只需要记住基地向量变换后的位置就好了！其他的向量都会随之而动！剩下都是标量的和基向量的运算了

上面变换的变换过程，在原有基向量的基础上！

分别沿着y轴伸长2倍，反向x轴伸长一倍，如果我们要计算线性变换过的向量的时候！那么标量其实是固定的，因为对应长度的缩放不会改变！

那么我们关注的应该是变换后的基向量！我们把变换后的两个基向量分别标记为ti tj

那么变换后的向量v 按照标量固定，他的线性组合计算就是 -1ti + 2tj

对于上面图所示的变换我们可以看出 ti 的位置在（ 1，-2） tj在 (3.0) 上

那么变换后的 v 向量从图上看 在 （5,2）的位置！

从计算的角度来看 -1ti + 2tj

$$\left. \begin{array} { l }{ - 1 \left[ \begin{array} { c } { 1 } \\ { - 2 } \end{array} \right] + 2 \left[ \begin{array} { l } { 3 } \\ { 0 } \end{array} \right] } { = \left[ \begin{array} { c } { - 1 } \\ { 4 } \end{array} \right] + \left[ \begin{array} { l } { 6 } \\ { 0 } \end{array} \right] } { = \left[ \begin{array} { c } { 5 } \\ { 2 } \end{array} \right] } \end{array} \right.$$

只要记录了变换后的ti tj你可以算出任意向量变换后的位置，这也是之前我在学习threejs的时候，一个向量乘以一个旋转矩阵就可以完成旋转效果的原因！

总结一下上面的公式 比如一个变换前的向量坐标是 （x,y）

$$\left. \begin{array} { l } { \left[ \begin{array} { l } { x } \\ { y } \end{array} \right] \rightarrow x \left[ \begin{array} { l } { 1 } \\ { - 2 } \end{array} \right] + y \left[ \begin{array} { l } { 3 } \\ { 0 } \end{array} \right] } { = \left[ \begin{array} { c } { 1 x + 3 y } \\ { - 2 x + 0 y } \end{array} \right] } \end{array} \right.$$

运用这个公式我们就可以输入任意一个向量，他就可以告诉你这个向量在变换后的位置！

以上推理我们可以说，变换后的任意向量我们可以仅由四个数字决定，变换后的ti tj坐标

我们通常把这些坐标包装到一个 2 * 2 的矩阵中！

$$\left[ \begin{array} { r r } { - 1 } & { 3 } \\ { 2 } & { 0 } \end{array} \right]$$

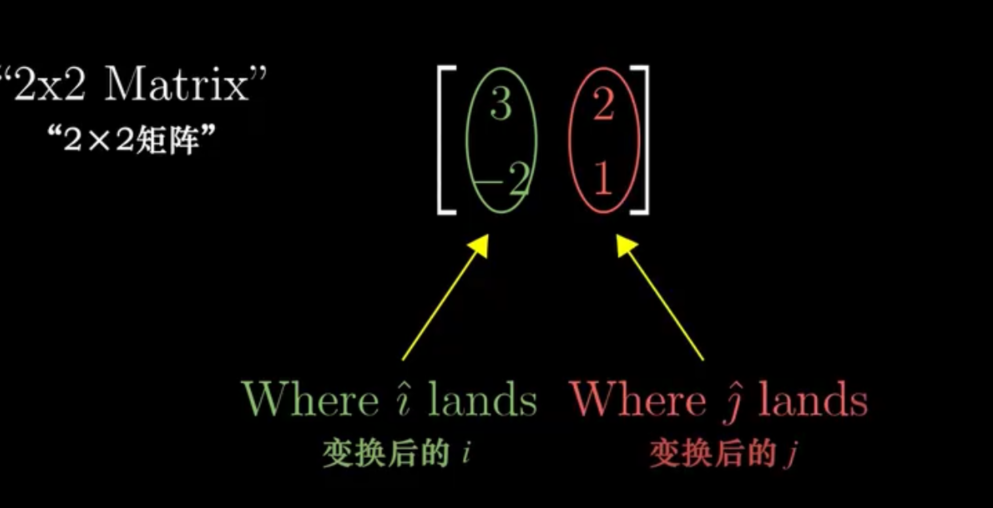
如果此时求一个任意向量变换后的位置，那么依旧套用上面的公式！

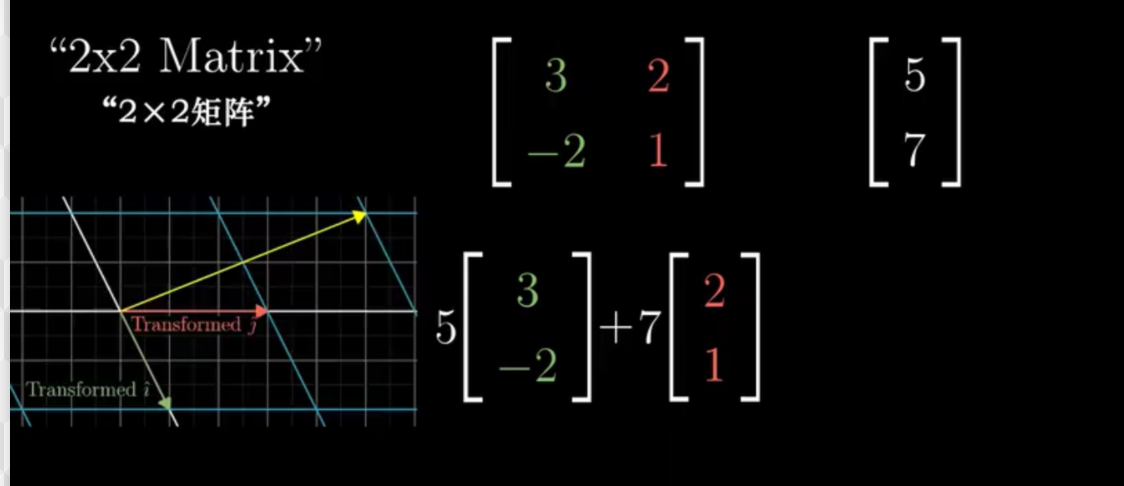
其实这里我们就可以推导出向量乘法的公式了 其实也是一个变换公式来的！

$$\left[ \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right] \left[ \begin{array} { l } { x } \\ { y } \end{array} \right] = x \left[ \begin{array} { l } { a } \\ { c } \end{array} \right] + y \left[ \begin{array} { l } { b } \\ { d } \end{array} \right] = \left[ \begin{array} { l } { a x + b y } \\ { c x + d y } \end{array} \right]$$

这像不像我们写代码的 函数定义呢？变换矩阵对应的我们的函数fx 传入要变换的矩阵 （x,y） 就是函数的参数，最后输出变换后的向量结果

$$f ( a ) = b$$

总结

总之线形变换是操作空间的一种手段！保证网格线平行且等距分布，且原点不动！

很好的是，我们通过基向量的这个概念就可以轻易的算出变换后任意向量的位置！