关于二叉树的遍历
以一定的顺序规则,逐个访问二叉树的所有结点,这个过程就是二叉树的遍历
按照顺序规则的不同,遍历方式有以下四种:
- 先序遍历
- 中序遍历
- 后序遍历
- 层次遍历
按照实现方式的不同,遍历方式又可以分为以下两种:
- 递归遍历(先、中、后序遍历)
- 迭代遍历(层次遍历)
递归遍历初相见
编程语言中,函数
Func(Type a,……)直接或间接调用函数本身,则该函数称为递归函数。
简单来说,当我们看到一个函数反复调用它自己的时候,递归就发生了。“递归”就意味着“反复”,像咱们之前对二叉树的定义,就可以理解为是一个递归式的定义:
- 它可以没有根结点,作为一棵空树存在
- 如果它不是空树,那么必须由根结点、左子树和右子树组成,且左右子树都是二叉树。
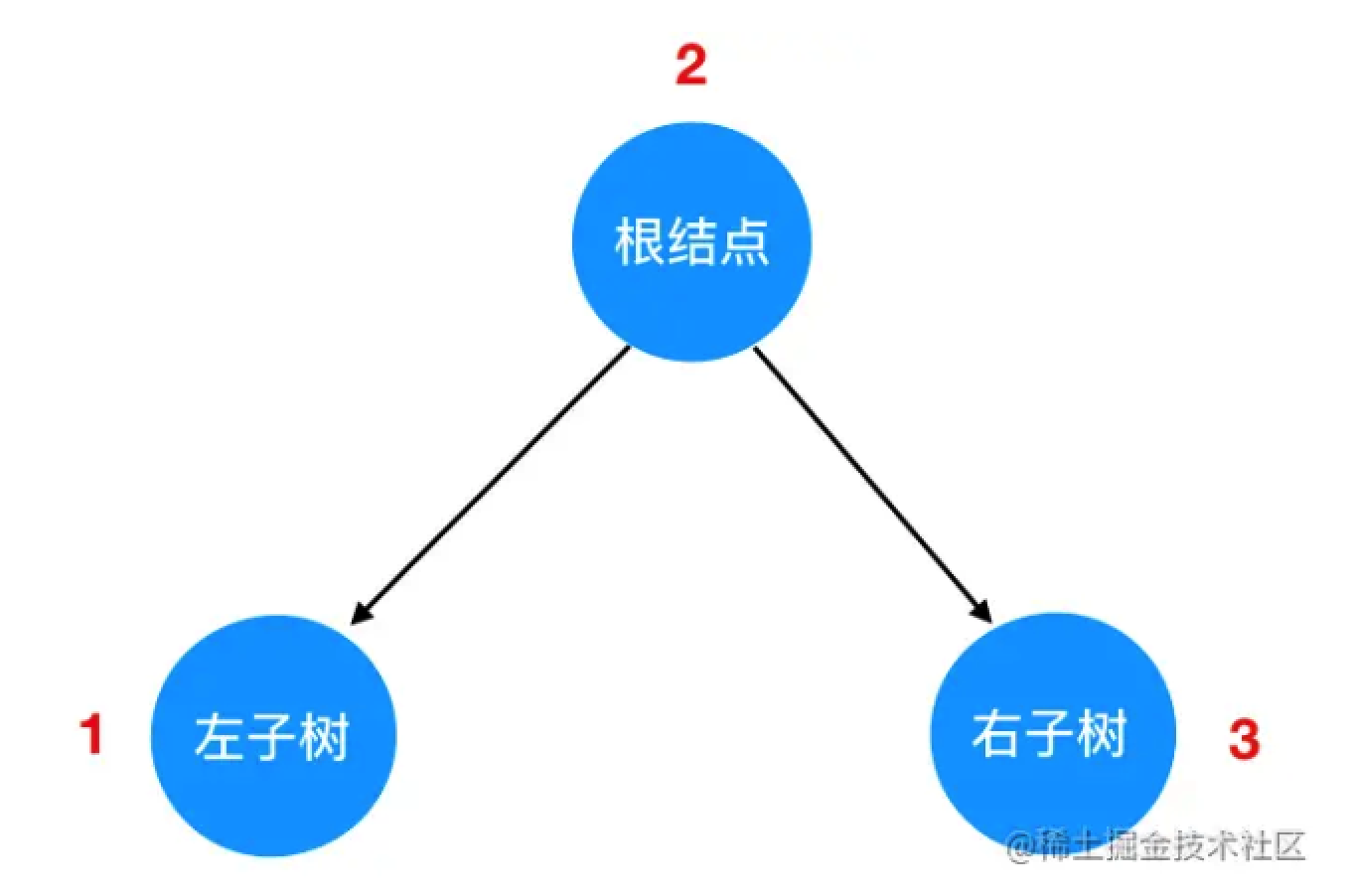
这个定义有着这样的内涵:如果我们想要创建一个二叉树结点作为根结点,那么它左侧的子结点和右侧的子结点也都必须符合二叉树结点的定义,这意味着我们要反复地执行“创建一个由数据域、左右子树组成的结点”这个动作,直到数据被分配完为止。 结合这个定义来看,每一棵二叉树都应该由这三部分组成:

对树的遍历,就可以看做是对这三个部分的遍历。这里就引出一个问题:三个部分中,到底先遍历哪个、后遍历哪个呢?
我们此处其实可以穷举一下,假如在保证“左子树一定先于右子树遍历”这个前提,那么遍历的可能顺序也不过三种:
- 根结点-> 左子树 -> 右子树 (先序遍历)
- 左子树 -> 根结点 -> 右子树 (中序遍历)
- 左子树 -> 右子树 ->根结点 (后序遍历)
上述三个遍历顺序,就分别对应了二叉树的先序遍历、中序遍历和后序遍历规则。在这三种顺序中,根结点的遍历分别被安排在了首要位置、中间位置和最后位置。
所谓的
“先序”、“中序”和“后序”,“先”、“中”、“后”其实就是指根结点的遍历时机。
先序遍历
先序遍历的“旅行路线”如下图

如果说有 N 多个子树,那么我们在每一棵子树内部,都要重复这个“旅行路线”,动画演示如下:

这个“重复”,我们就用递归来实现。
上面这个二叉树的结构,用JavaScript的代码表示
const root = {
val: "A",
left: {
val: "B",
left: {
val: "D"
},
right: {
val: "E"
}
},
right: {
val: "C",
right: {
val: "F"
}
}
};
编写一个递归函数之前,大家首先要明确两样东西:
-
递归式
递归式,它指的是你每一次重复的内容是什么。
在这里,我们要做先序遍历,那么每一次重复的其实就是根结点 -> 左子树 -> 右子树这个旅行路线。 -
递归边界
递归边界,它指的是你什么时候停下来。
在遍历的场景下,当我们发现遍历的目标树为空的时候,就意味着旅途已达终点、需要画上句号了。这个“画句号”的方式,在编码实现里对应着一个return语句——这就是二叉树遍历的递归边界。
上面咱们已经捋清楚思路,接下来话不多说,先序遍历的编码实现:
// 所有遍历函数的入参都是树的根结点对象
function preorder(root) {
// 递归边界,root 为空
if(!root) {
return
}
// 输出当前遍历的结点值
console.log('当前遍历的结点值是:', root.val)
// 递归遍历左子树
preorder(root.left)
// 递归遍历右子树
preorder(root.right)
}
放到控制台输出一下瞅瞅!
当前遍历的结点值是: A
当前遍历的结点值是: B
当前遍历的结点值是: D
当前遍历的结点值是: E
当前遍历的结点值是: C
当前遍历的结点值是: F
去和上面的图对一下,看看是不是一样!

中序遍历
理解了先序遍历的过程,中序遍历就不是什么难题。唯一的区别只是把遍历顺序调换了左子树 -> 根结点 -> 右子树:
若有多个子树,那么我们在每一棵子树内部,都要重复这个“旅行路线”,这个过程用动画表示如下:
递归边界照旧,唯一发生改变的是递归式里调用递归函数的顺序——左子树的访问会优先于根结点。我们参考先序遍历的分析思路,来写中序遍历的代码:
// 所有遍历函数的入参都是树的根结点对象
function preorder(root) {
// 递归边界,root 为空
if (!root) {
return
}
// 1递归遍历左子树
preorder(root.left)
// 2 输出当前遍历的结点值 (这里就代表对节点的操作!优先操作这里的节点!)
console.log('当前遍历的结点值是:', root.val)
// 3递归遍历右子树
preorder(root.right)
}
丢在控制台输出的结果,和预期一致!
当前遍历的结点值是: D
当前遍历的结点值是: B
当前遍历的结点值是: E
当前遍历的结点值是: A
当前遍历的结点值是: C
当前遍历的结点值是: F
后序遍历
在后序遍历中,我们先访问左子树,再访问右子树,最后访问根结点:

若有多个子树,那么我们在每一棵子树内部,都要重复这个“旅行路线”:
在编码实现的时候,递归边界照旧,唯一发生改变的仍然是是递归式里调用递归函数的顺序:
// 所有遍历函数的入参都是树的根结点对象
function preorder(root) {
// 递归边界,root 为空
if (!root) {
return
}
// 1递归遍历左子树
preorder(root.left)
// 2递归遍历右子树
preorder(root.right)
// 3 输出当前遍历的结点值 (这里就代表对节点的操作!优先操作这里的节点!)
console.log('当前遍历的结点值是:', root.val)
}
丢到控制台的输出结果:
当前遍历的结点值是: D
当前遍历的结点值是: E
当前遍历的结点值是: B
当前遍历的结点值是: F
当前遍历的结点值是: C
当前遍历的结点值是: A
到这里其实还是蛮简单的哈!



评论区